IN DEPTH ANALYSIS
All about Feature Scaling
Scale data for better performance of Machine Learning Model
Machine learning is like making a mixed fruit juice. If we want to get the best-mixed juice, we need to mix all fruit not by their size but based on their right proportion. We just need to remember apple and strawberry are not the same unless we make them similar in some context to compare their attribute. Similarly, in many machine learning algorithms, to bring all features in the same standing, we need to do scaling so that one significant number doesn’t impact the model just because of their large magnitude.
Feature scaling in machine learning is one of the most critical steps during the pre-processing of data before creating a machine learning model. Scaling can make a difference between a weak machine learning model and a better one.
The most common techniques of feature scaling are Normalization and Standardization.
Normalization is used when we want to bound our values between two numbers, typically, between [0,1] or [-1,1]. While Standardization transforms the data to have zero mean and a variance of 1, they make our data unitless. Refer to the below diagram, which shows how data looks after scaling in the X-Y plane.

Why do we need scaling?
Machine learning algorithm just sees number — if there is a vast difference in the range say few ranging in thousands and few ranging in the tens, and it makes the underlying assumption that higher ranging numbers have superiority of some sort. So these more significant number starts playing a more decisive role while training the model.
The machine learning algorithm works on numbers and does not know what that number represents. A weight of 10 grams and a price of 10 dollars represents completely two different things — which is a no brainer for humans, but for a model as a feature, it treats both as same.
Suppose we have two features of weight and price, as in the below table. The “Weight” cannot have a meaningful comparison with the “Price.” So the assumption algorithm makes that since “Weight” > “Price,” thus “Weight,” is more important than “Price.”

So these more significant number starts playing a more decisive role while training the model. Thus feature scaling is needed to bring every feature in the same footing without any upfront importance. Interestingly, if we convert the weight to “Kg,” then “Price” becomes dominant.
Another reason why feature scaling is applied is that few algorithms like Neural network gradient descent converge much faster with feature scaling than without it.

One more reason is saturation, like in the case of sigmoid activation in Neural Network, scaling would help not to saturate too fast.
When to do scaling?
Feature scaling is essential for machine learning algorithms that calculate distances between data. If not scale, the feature with a higher value range starts dominating when calculating distances, as explained intuitively in the “why?” section.
The ML algorithm is sensitive to the “relative scales of features,” which usually happens when it uses the numeric values of the features rather than say their rank.
In many algorithms, when we desire faster convergence, scaling is a MUST like in Neural Network.
Since the range of values of raw data varies widely, in some machine learning algorithms, objective functions do not work correctly without normalization. For example, the majority of classifiers calculate the distance between two points by the distance. If one of the features has a broad range of values, the distance governs this particular feature. Therefore, the range of all features should be normalized so that each feature contributes approximately proportionately to the final distance.
Even when the conditions, as mentioned above, are not satisfied, you may still need to rescale your features if the ML algorithm expects some scale or a saturation phenomenon can happen. Again, a neural network with saturating activation functions (e.g., sigmoid) is a good example.
Rule of thumb we may follow here is an algorithm that computes distance or assumes normality, scales your features.
Some examples of algorithms where feature scaling matters are:
- K-nearest neighbors (KNN) with a Euclidean distance measure is sensitive to magnitudes and hence should be scaled for all features to weigh in equally.
- K-Means uses the Euclidean distance measure here feature scaling matters.
- Scaling is critical while performing Principal Component Analysis(PCA). PCA tries to get the features with maximum variance, and the variance is high for high magnitude features and skews the PCA towards high magnitude features.
- We can speed up gradient descent by scaling because θ descends quickly on small ranges and slowly on large ranges, and oscillates inefficiently down to the optimum when the variables are very uneven.
Algorithms that do not require normalization/scaling are the ones that rely on rules. They would not be affected by any monotonic transformations of the variables. Scaling is a monotonic transformation. Examples of algorithms in this category are all the tree-based algorithms — CART, Random Forests, Gradient Boosted Decision Trees. These algorithms utilize rules (series of inequalities) and do not require normalization.
Algorithms like Linear Discriminant Analysis(LDA), Naive Bayes is by design equipped to handle this and give weights to the features accordingly. Performing features scaling in these algorithms may not have much effect.
Few key points to note :
- Mean centering does not affect the covariance matrix
- Scaling of variables does affect the covariance matrix
- Standardizing affects the covariance
How to perform feature scaling?
Below are the few ways we can do feature scaling.
1) Min Max Scaler
2) Standard Scaler
3) Max Abs Scaler
4) Robust Scaler
5) Quantile Transformer Scaler
6) Power Transformer Scaler
7) Unit Vector Scaler
For the explanation, we will use the table shown in the top and form the data frame to show different scaling methods.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
df = pd.DataFrame({'WEIGHT': [15, 18, 12,10],
'PRICE': [1,3,2,5]},
index = ['Orange','Apple','Banana','Grape'])
print(df)WEIGHT PRICE
Orange 15 1
Apple 18 3
Banana 12 2
Grape 10 5
1)Min-Max scaler
Transform features by scaling each feature to a given range. This estimator scales and translates each feature individually such that it is in the given range on the training set, e.g., between zero and one. This Scaler shrinks the data within the range of -1 to 1 if there are negative values. We can set the range like [0,1] or [0,5] or [-1,1].
This Scaler responds well if the standard deviation is small and when a distribution is not Gaussian. This Scaler is sensitive to outliers.
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()df1 = pd.DataFrame(scaler.fit_transform(df),
columns=['WEIGHT','PRICE'],
index = ['Orange','Apple','Banana','Grape'])ax = df.plot.scatter(x='WEIGHT', y='PRICE',color=['red','green','blue','yellow'],
marker = '*',s=80, label='BREFORE SCALING');df1.plot.scatter(x='WEIGHT', y='PRICE', color=['red','green','blue','yellow'],
marker = 'o',s=60,label='AFTER SCALING', ax = ax);plt.axhline(0, color='red',alpha=0.2)
plt.axvline(0, color='red',alpha=0.2);

2) Standard Scaler
The Standard Scaler assumes data is normally distributed within each feature and scales them such that the distribution centered around 0, with a standard deviation of 1.
Centering and scaling happen independently on each feature by computing the relevant statistics on the samples in the training set. If data is not normally distributed, this is not the best Scaler to use.
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
df2 = pd.DataFrame(scaler.fit_transform(df),
columns=['WEIGHT','PRICE'],
index = ['Orange','Apple','Banana','Grape'])
ax = df.plot.scatter(x='WEIGHT', y='PRICE',color=['red','green','blue','yellow'],
marker = '*',s=80, label='BREFORE SCALING');
df2.plot.scatter(x='WEIGHT', y='PRICE', color=['red','green','blue','yellow'],
marker = 'o',s=60,label='AFTER SCALING', ax = ax)
plt.axhline(0, color='red',alpha=0.2)
plt.axvline(0, color='red',alpha=0.2);
3) Max Abs Scaler
Scale each feature by its maximum absolute value. This estimator scales and translates each feature individually such that the maximal absolute value of each feature in the training set is 1.0. It does not shift/center the data and thus does not destroy any sparsity.
On positive-only data, this Scaler behaves similarly to Min Max Scaler and, therefore, also suffers from the presence of significant outliers.
from sklearn.preprocessing import MaxAbsScaler
scaler = MaxAbsScaler()
df4 = pd.DataFrame(scaler.fit_transform(df),
columns=['WEIGHT','PRICE'],
index = ['Orange','Apple','Banana','Grape'])
ax = df.plot.scatter(x='WEIGHT', y='PRICE',color=['red','green','blue','yellow'],
marker = '*',s=80, label='BREFORE SCALING');
df4.plot.scatter(x='WEIGHT', y='PRICE', color=['red','green','blue','yellow'],
marker = 'o',s=60,label='AFTER SCALING', ax = ax)
plt.axhline(0, color='red',alpha=0.2)
plt.axvline(0, color='red',alpha=0.2);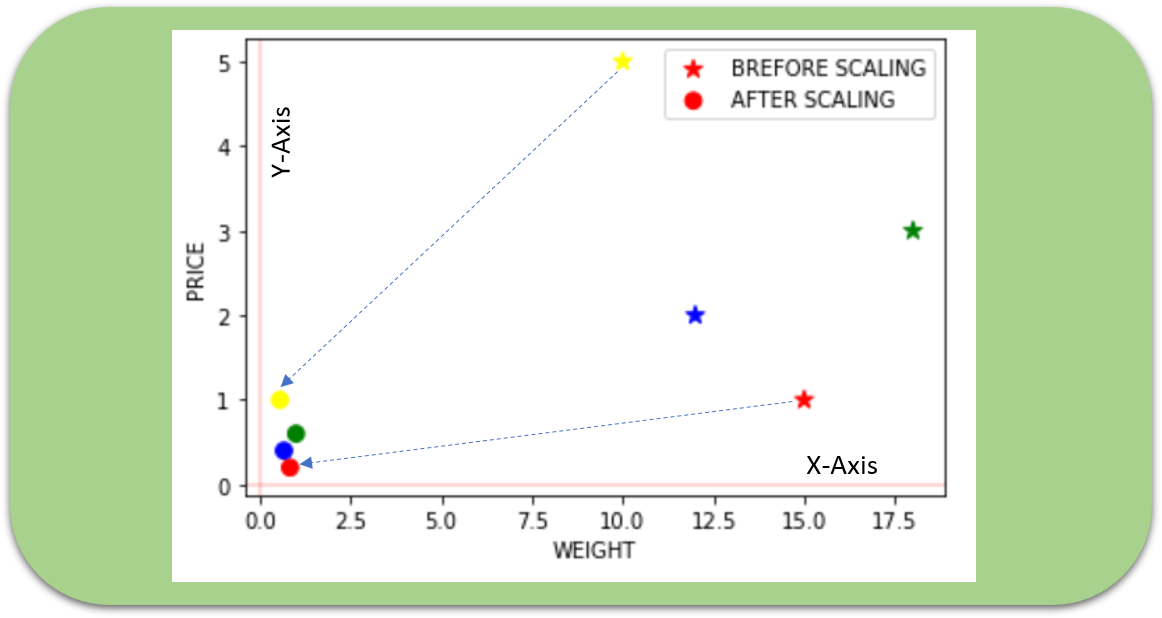
4) Robust Scaler
As the name suggests, this Scaler is robust to outliers. If our data contains many outliers, scaling using the mean and standard deviation of the data won’t work well.
This Scaler removes the median and scales the data according to the quantile range (defaults to IQR: Interquartile Range). The IQR is the range between the 1st quartile (25th quantile) and the 3rd quartile (75th quantile). The centering and scaling statistics of this Scaler are based on percentiles and are therefore not influenced by a few numbers of huge marginal outliers. Note that the outliers themselves are still present in the transformed data. If a separate outlier clipping is desirable, a non-linear transformation is required.
from sklearn.preprocessing import RobustScaler
scaler = RobustScaler()
df3 = pd.DataFrame(scaler.fit_transform(df),
columns=['WEIGHT','PRICE'],
index = ['Orange','Apple','Banana','Grape'])
ax = df.plot.scatter(x='WEIGHT', y='PRICE',color=['red','green','blue','yellow'],
marker = '*',s=80, label='BREFORE SCALING');
df3.plot.scatter(x='WEIGHT', y='PRICE', color=['red','green','blue','yellow'],
marker = 'o',s=60,label='AFTER SCALING', ax = ax)
plt.axhline(0, color='red',alpha=0.2)
plt.axvline(0, color='red',alpha=0.2);
Let’s now see what happens if we introduce an outlier and see the effect of scaling using Standard Scaler and Robust Scaler (a circle shows outlier).
dfr = pd.DataFrame({'WEIGHT': [15, 18, 12,10,50],
'PRICE': [1,3,2,5,20]},
index = ['Orange','Apple','Banana','Grape','Jackfruit'])
print(dfr)
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
df21 = pd.DataFrame(scaler.fit_transform(dfr),
columns=['WEIGHT','PRICE'],
index = ['Orange','Apple','Banana','Grape','Jackfruit'])
ax = dfr.plot.scatter(x='WEIGHT', y='PRICE',color=['red','green','blue','yellow','black'],
marker = '*',s=80, label='BREFORE SCALING');
df21.plot.scatter(x='WEIGHT', y='PRICE', color=['red','green','blue','yellow','black'],
marker = 'o',s=60,label='STANDARD', ax = ax,figsize=(12,6))
from sklearn.preprocessing import RobustScaler
scaler = RobustScaler()
df31 = pd.DataFrame(scaler.fit_transform(dfr),
columns=['WEIGHT','PRICE'],
index = ['Orange','Apple','Banana','Grape','Jackfruit'])df31.plot.scatter(x='WEIGHT', y='PRICE', color=['red','green','blue','yellow','black'],
marker = 'v',s=60,label='ROBUST', ax = ax,figsize=(12,6))
plt.axhline(0, color='red',alpha=0.2)
plt.axvline(0, color='red',alpha=0.2);WEIGHT PRICE
Orange 15 1
Apple 18 3
Banana 12 2
Grape 10 5
Jackfruit 50 20

5) Quantile Transformer Scaler
Transform features using quantiles information.
This method transforms the features to follow a uniform or a normal distribution. Therefore, for a given feature, this transformation tends to spread out the most frequent values. It also reduces the impact of (marginal) outliers: this is, therefore, a robust pre-processing scheme.
The cumulative distribution function of a feature is used to project the original values. Note that this transform is non-linear and may distort linear correlations between variables measured at the same scale but renders variables measured at different scales more directly comparable. This is also sometimes called as Rank scaler.
from sklearn.preprocessing import QuantileTransformer
scaler = QuantileTransformer()
df6 = pd.DataFrame(scaler.fit_transform(df),
columns=['WEIGHT','PRICE'],
index = ['Orange','Apple','Banana','Grape'])
ax = df.plot.scatter(x='WEIGHT', y='PRICE',color=['red','green','blue','yellow'],
marker = '*',s=80, label='BREFORE SCALING');
df6.plot.scatter(x='WEIGHT', y='PRICE', color=['red','green','blue','yellow'],
marker = 'o',s=60,label='AFTER SCALING', ax = ax,figsize=(6,4))
plt.axhline(0, color='red',alpha=0.2)
plt.axvline(0, color='red',alpha=0.2);
The above example is just for illustration as Quantile transformer is useful when we have a large dataset with many data points usually more than 1000.
6) Power Transformer Scaler
The power transformer is a family of parametric, monotonic transformations that are applied to make data more Gaussian-like. This is useful for modeling issues related to the variability of a variable that is unequal across the range (heteroscedasticity) or situations where normality is desired.
The power transform finds the optimal scaling factor in stabilizing variance and minimizing skewness through maximum likelihood estimation. Currently, Sklearn implementation of PowerTransformer supports the Box-Cox transform and the Yeo-Johnson transform. The optimal parameter for stabilizing variance and minimizing skewness is estimated through maximum likelihood. Box-Cox requires input data to be strictly positive, while Yeo-Johnson supports both positive or negative data.
from sklearn.preprocessing import PowerTransformer
scaler = PowerTransformer(method='yeo-johnson')
df5 = pd.DataFrame(scaler.fit_transform(df),
columns=['WEIGHT','PRICE'],
index = ['Orange','Apple','Banana','Grape'])
ax = df.plot.scatter(x='WEIGHT', y='PRICE',color=['red','green','blue','yellow'],
marker = '*',s=80, label='BREFORE SCALING');
df5.plot.scatter(x='WEIGHT', y='PRICE', color=['red','green','blue','yellow'],
marker = 'o',s=60,label='AFTER SCALING', ax = ax)
plt.axhline(0, color='red',alpha=0.2)
plt.axvline(0, color='red',alpha=0.2);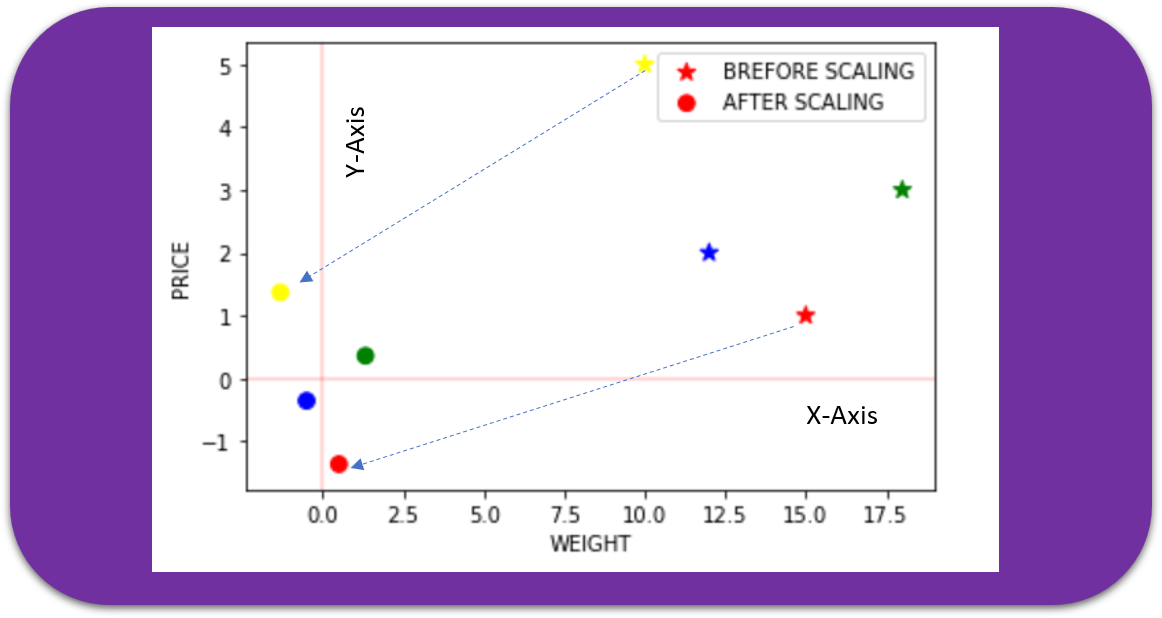
7) Unit Vector Scaler

Scaling is done considering the whole feature vector to be of unit length. This usually means dividing each component by the Euclidean length of the vector (L2 Norm). In some applications (e.g., histogram features), it can be more practical to use the L1 norm of the feature vector.
Like Min-Max Scaling, the Unit Vector technique produces values of range [0,1]. When dealing with features with hard boundaries, this is quite useful. For example, when dealing with image data, the colors can range from only 0 to 255.

If we plot, then it would look as below for L1 and L2 norm, respectively.

The below diagram shows how data spread for all different scaling techniques, and as we can see, a few points are overlapping, thus not visible separately.

Final Note:
Feature scaling is an essential step in Machine Learning pre-processing. Deep learning requires feature scaling for faster convergence, and thus it is vital to decide which feature scaling to use. There are many comparison surveys of scaling methods for various algorithms. Still, like most other machine learning steps, feature scaling too is a trial and error process, not a single silver bullet.
I look forward to your comment and share if you have any unique experience related to feature scaling. Thanks for reading. You can connect me @LinkedIn.
Reference:
http://sebastianraschka.com/Articles/2014_about_feature_scaling.html
https://www.kdnuggets.com/2019/04/normalization-vs-standardization-quantitative-analysis.html
WRITTEN BY












No comments:
Post a Comment